Functional equivalence

Robert P. Webber, Don Blaheta, Longwood University
Why are we working on this? When there is more than one way to solve a problem—as there often is—we typically want to find a simple one, but we also need to prove that it works. In the realm of circuit design, we use functional equivalence to demonstrate that one circuit does the same job as another. Skills in this section: Use truth tables to compare the output expected for different circuits or expressions Concepts: Algorithm representation

Recall that one of the gates for which we have defined a truth table is called nor:

A B A nor B
0 0 1
0 1 0
1 0 0
1 1 0

We can construct other circuits whose output column is the same as that for nor For instance, consider the function

(not A) and (not B)

We can derive its truth table as follows:

A B not A not B (not A) and (not B)
0 0 1 1 1
0 1 1 0 0
1 0 0 1 0
1 1 0 0 0

Notice the final column is the same as the nor table! We can put them together in the same table to be extra clear about this:

↓ ↓
A B not A not B (not A) and (not B) A nor B
0 0 1 1 1 1
0 1 1 0 0 0
1 0 0 1 0 0
1 1 0 0 0 0

This is one way to conclusively show that two circuits are functionally equivalent. That is, the two expressions compute the same function: for any set of valid inputs, both expressions will produce exactly the same output. We sometimes use the symbol "⇔" to indicate that two expressions are equivalent:

A nor B ⇔ (not A) and (not B)

We have also previously stated that nor can be defined as a combination of not with or, and we can use our new notation to express this directly:
A nor B ⇔ not (A or B)

We can prove it, too:
↓ ↓
A B A nor B A or B not (A or B)
0 0 1 0 1
0 1 0 1 0
1 0 0 1 0
1 1 0 1 0

Furthermore, since we've found two different expressions each equivalent to A nor B, those two expressions are also functionally equivalent to each other:

not (A or B) ⇔ (not A) and (not B)

We can determine whether any two logical functions are equivalent by comparing their truth tables. The functions are equivalent if and only if the truth values are the same.

Functional completeness

We have seen a total of six gates defined, but for an electrical engineer trying to design hardware, it isn't actually necessary to build all six gates. Some of them can be written as combinations of others. For instance, we have already seen that nor can be written as a combination of not and and gates:

A nor B ⇔ (not A) and (not B)

If we have two not gates and one and gate, we can build a circuit that will perform the nor function.

Similarly, we can write nand and xor as combinations of and, or, and not gates (Exercises 9 and 11). This means that the set of gates {and, or, not} is functionally complete, because the other basic gates (and indeed, any logical circuit) can be built from only these three gates.

Are there other functionally complete sets of gates? The answer is yes. Indeed, and can be written as a combination of or and not:

A and B ⇔ not ((not A) or (not B)) ,

which you can verify using a truth table. So {not, or} is functionally complete.

Similarly, or can be written as a combination of and and not.

A or B ⇔ not ((not A) and (not B)) ,

so {not, and} is functionally complete.

Surprisingly, {nand} by itself is functionally complete!

not A ⇔ A nand A

A and B ⇔ (A nand B) nand (A nand B) (Exercise 12)

A or B ⇔ (A nand A) nand (B nand B) (Exercise 13)

Similarly, {nor} is a functionally complete set. This means that a computer engineer with a big supply of nand or nor gates could theoretically build the most powerful computer in the world.

Exercises

  1. Are the following circuits functionally equivalent?
  2. Are the following circuits functionally equivalent?
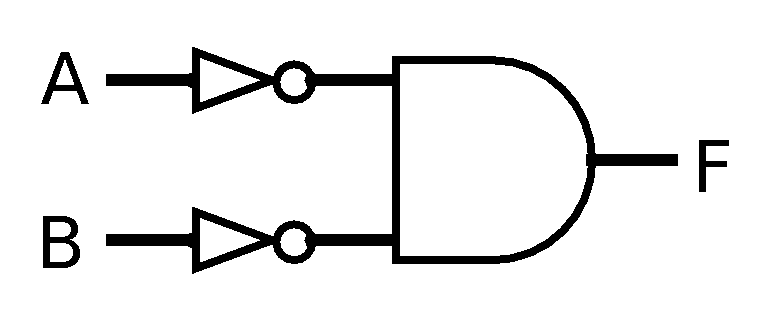
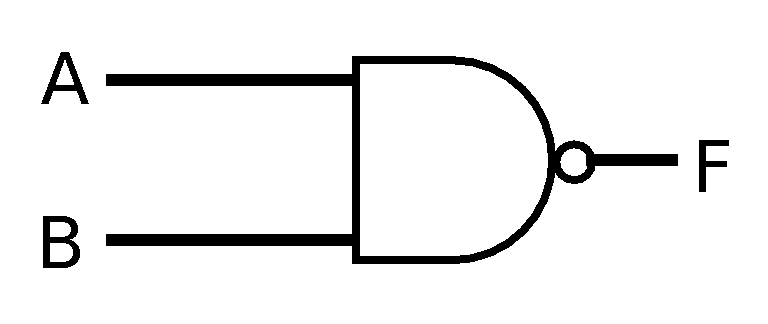
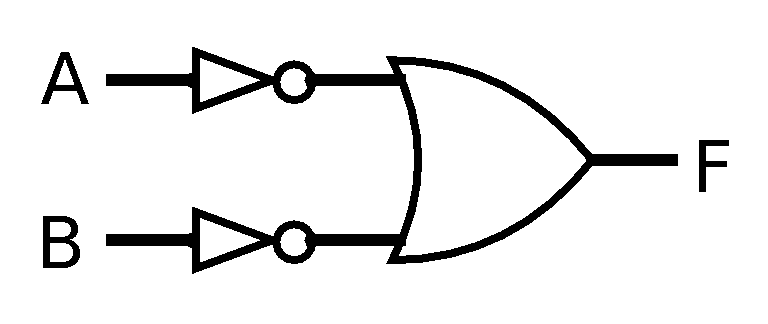
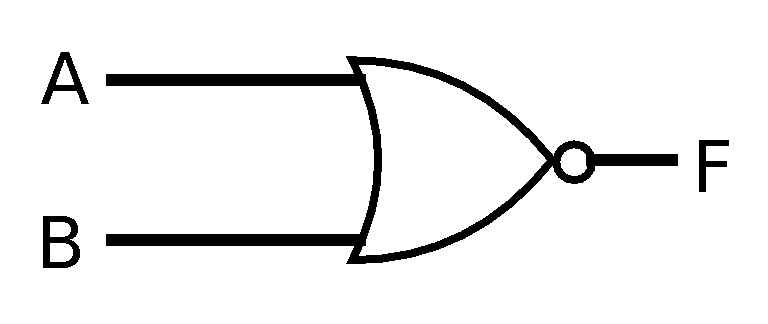
  3. Are the circuits x and x and x functionally equivalent?

  4. Are the circuits x or (x and y) and x functionally equivalent?

  5. Are the circuits not (A or B) and (not A) or (not B) functionally equivalent?

  6. Are the circuits not ( A and B) and (not A) or (not B) functionally equivalent?

  7. Are the circuits x and (not y), and (not x) or y, functionally equivalent?

  8. Are the circuits (not z) or ((not y) and x), and (x and (not z)) or (not (y or z)), functionally equivalent?

  9. Design a circuit that is functionally equivalent to a NAND gate using only AND, OR, and NOT gates.

  10. Design a circuit that is functionally equivalent to a NOR gate using only AND, OR, and NOT gates.

  11. Design a circuit that is functionally equivalent to a XOR gate using only AND, OR, and NOT gates.

  12. Design a circuit that is functionally equivalent to an AND gate using only NAND gates.

  13. Design a circuit that is functionally equivalent to an OR gate using only NAND gates.

Credits and licensing

This article is by Robert P. Webber and Don Blaheta, licensed under a Creative Commons BY-SA 3.0 license.

Version 2016-Mar-23 01:00