Evaluating circuits
Each of the standard digital logic gates can be combined with others to represent various computations. These computations are often referred to as circuits and can be drawn graphically by connecting the inputs of one gate to the outputs of another, as in this example:
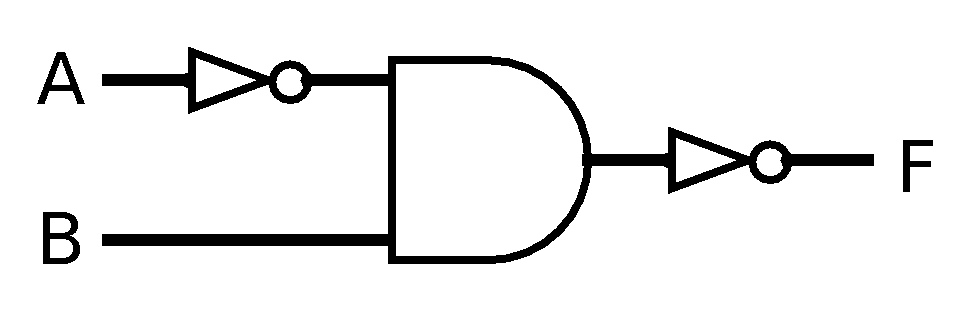 |
The usual convention (which we follow in all of our diagrams) is to draw the inputs on the left and label them, and then to connect the gates so that all data flows left-to-right, ending in the circuit's output on the right side of the diagram (often also labelled). So in the above diagram, the input labelled A flows into a not gate. The output of that gate, together with the input labelled B, flows into an and gate. Finally, the output of that gate goes through a second not gate, whose output is the output of the entire circuit, labelled F.
We have previously seen what a truth table looks like, and so we could hope to report the behavior of this circuit in a truth table:
| A | B | F |
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
But how can we figure out what the value of F is for various input combinations? One way is to actually build the circuit, either physically or in a simulator such as Logisim, and then try each combination of values for A and B. You could also simulate the circuit by hand using the above drawing. But we'd like to come up with a more systematic way, and to do that we're going to first talk about how to represent circuits in expression form.
Gate logic expressions
Every kind of gate has a name—the three we've seen so far are and, or, and not. If we have a complete circuit diagram, we can convert it into a written expression by starting with the labelled inputs on the left, and then writing the result of applying each gate in turn to its inputs. We can start with the first gate, in the upper left of the diagram:
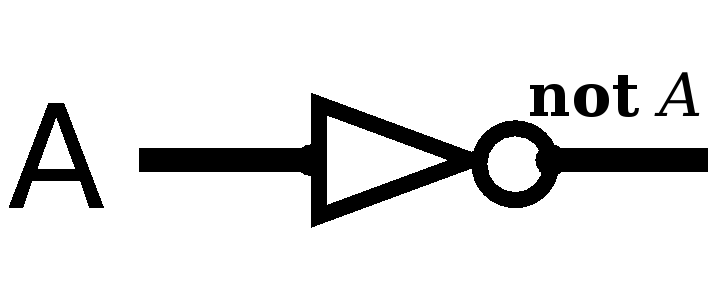 |
Its input is just the labelled input A, and it is a not gate, so the output of this little sub-circuit is labelled "not A". We then walk through the circuit labelling the output of each gate. If the gate's input was anything more complex than a single-letter original input, we put parentheses around it for clarity:
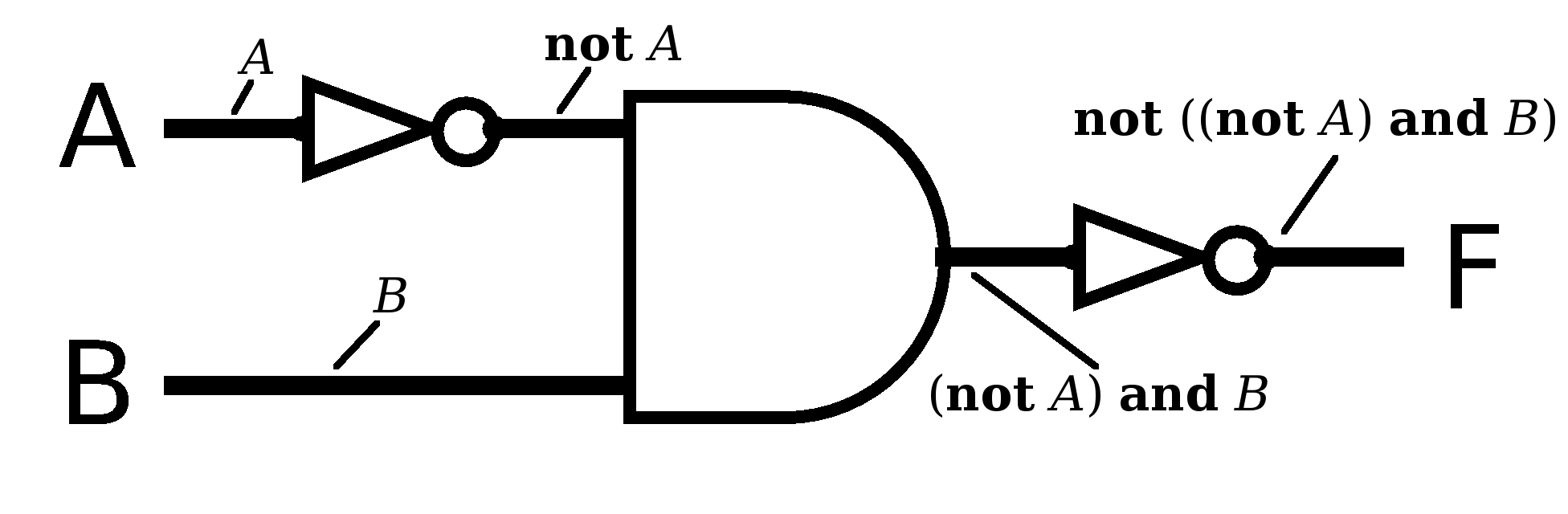 |
So our original circuit diagram corresponds to the gate logic expression
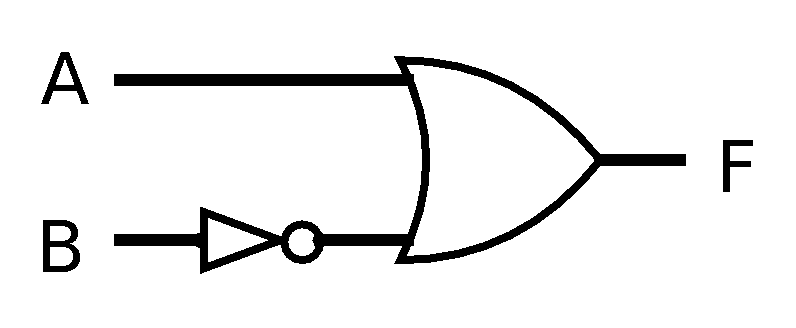 |
Here, the input to the or gate needs to be (not B), which is provided by the not gate fed by the input B.
Evaluating using truth tables
To return to our original example, we wish to compute a truth table that evaluates all outputs for the following circuit:
 |
| not ((not A) and B) |
Much as we do when evaluating an arithmetic expression, we can break down this gate logic expression by looking at the innermost parts first, and evaluating them—for each possible input—before using those values to contribute to the larger expression. We can organize our work on this by progressively adding columns to a truth table. In this case, the first relevant piece to evaluate would be not A, so we add that first:
| A | B | not A |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Next we add the result of the and, and finally the result of the whole expression:
| A | B | not A | (not A) and B | not ((not A) and B) |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
What if we are presented with a circuit that has three inputs?
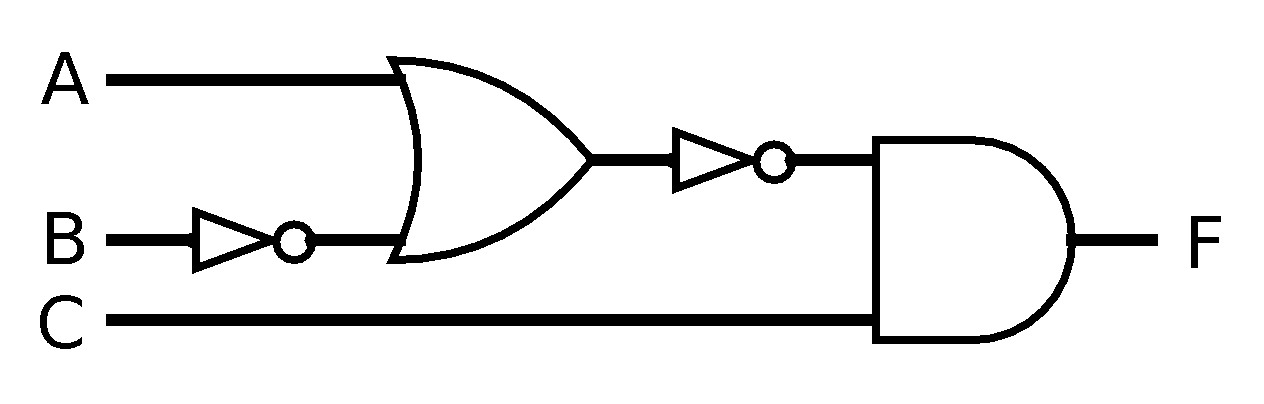 |
We can apply the same analytical process, but first we need a truth table with more rows, as there are more than four possible combinations of input values when there are three inputs. In fact, there will be twice as many as before: for every combination of A and B, we could imagine that C is 0, so that's four combinations, and for each of those combinations of A and B we could also imagine that C is 1, for another four combinations.
And it's not a coincidence that a circuit with 3 inputs will require an 8-row truth table. In general, a truth table meant to evaluate a circuit with n inputs will require 2n rows—for exactly the same reason that a data representation with n bits can represent 2n distinct values. We can use that information to organize our truth table as we build it:
| A | B | C |
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
If we look at the three columns as bits in a binary number, this order has us counting from 000 to 111—that is, from 0 to 7—and so we can be confident that we haven't missed any cases. To evaluate the circuit, we start with the “innermost” pieces of the expression, which correspond to the gates on the left side of the diagram:
| A | B | C | not B | A or (not B) |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
We continue left to right through the circuit to compute the last two columns:
| A | B | C | not B | A or (not B) | not (A or (not B)) | (not (A or (not B))) and C |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
“Splitting” inputs
As our gate logic expressions get more complicated, we will start to see some where the same letter, representing a single input, appears more than once. Consider the following expression:
If we were to draw up a circuit diagram to represent that circuit, following the principles laid out above, we might hazard the following reasonable guess:
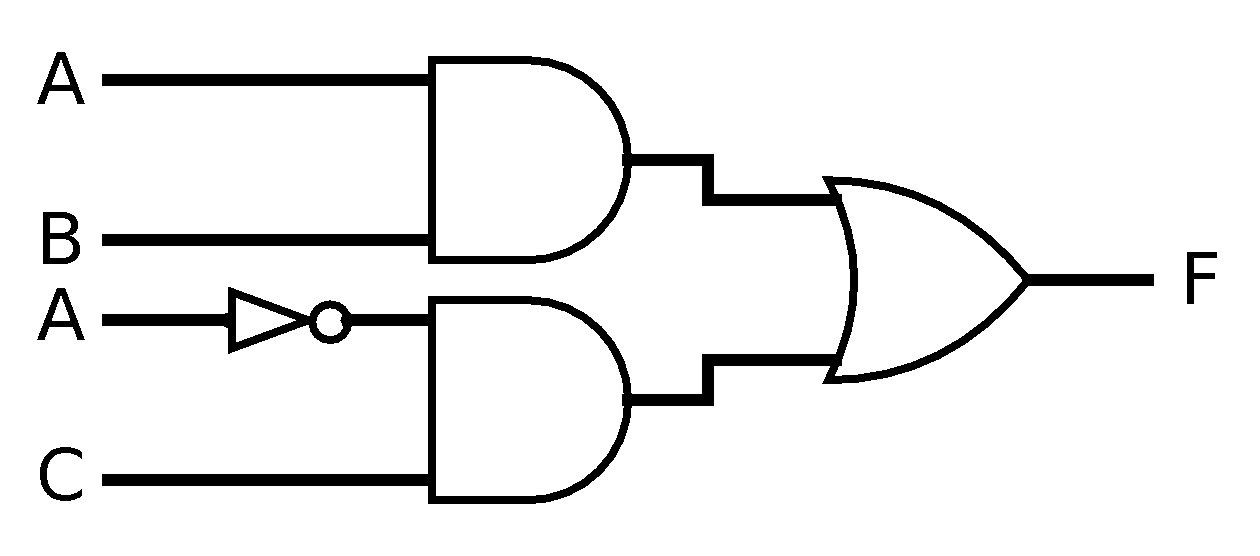 |
| A reasonable, though incorrect, guess |
The problem with this diagram is that it has two different inputs labelled A. In the written expression, the letter itself is the only way to indicate the sameness of an input—A might be either 0 or 1 but it must hold the same value throughout the expression—but in a visual diagram, we represent the idea that a single input gets used in multiple places in the circuit by “splitting” the input. In the diagram, we draw a dot where the split occurs, and an additional line going in another direction, like so:
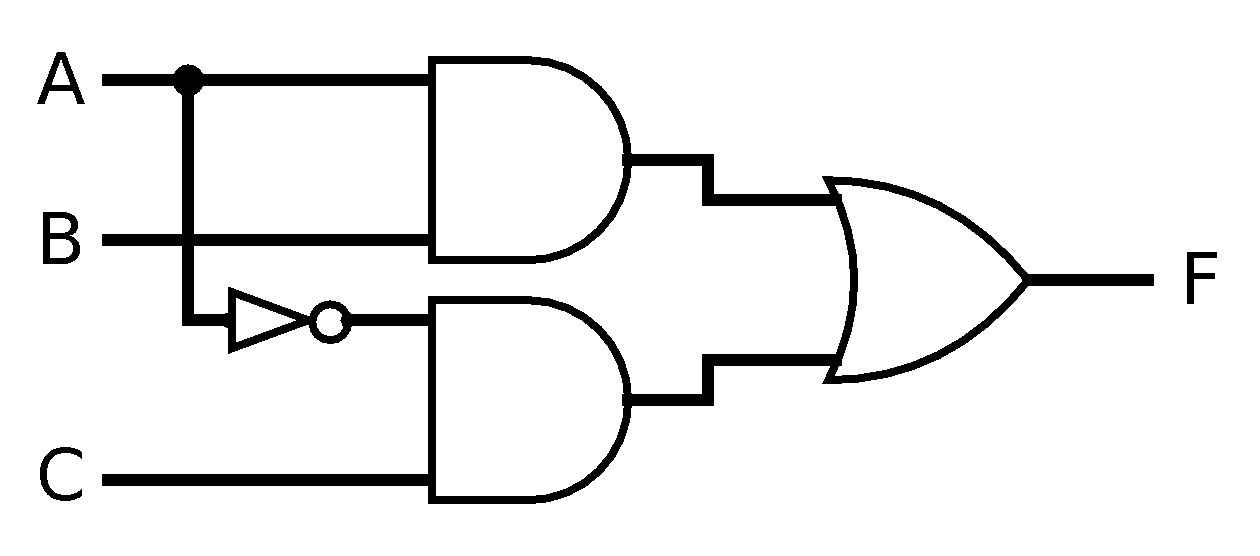 |
| (A and B) or ((not A) and C) |
Note that lines can cross without interfering with each other, if no dot is drawn there, as shown when the line coming down from A crosses over the line for B. Note also that this only works when one input is split into multiple wires; if you connect two wires that would represent two inputs joining together, its meaning is unclear and it makes for an invalid diagram (and an invalid circuit):
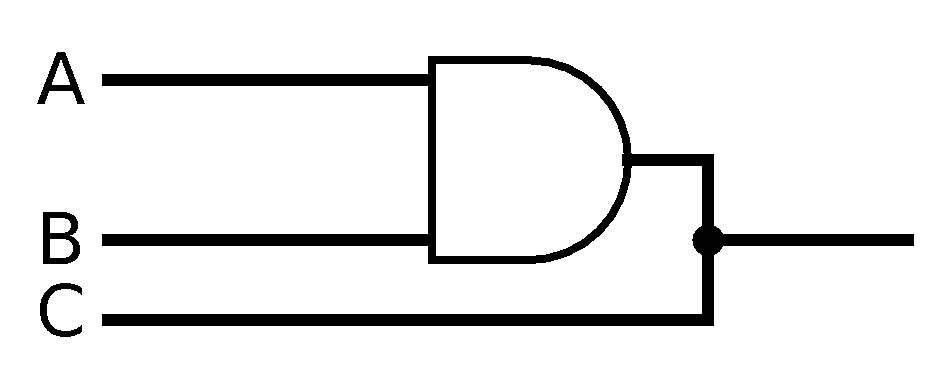 |
| Invalid joining from two sources |
How would you determine what the value of that wire should be, if its inputs were different? There's no single coherent answer, and you can always disambiguate your intent by putting a gate there, so that's what we require. The corresponding expression would be something like (A and B) ??? C, and once you know whether you want the ??? to be and or or or something else, just say so.
Additional gates
There are a few additional functions of two inputs which turn up with some regularity in computer science and electrical engineering, and which have been given their own names and symbols. The first, called nand, is precisely the negation of and:
| A | B | A and B | A nand B |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
You might see that nand is a contraction of not and, and could certainly be imitated with an and gate plus a not gate. But it does have its own name, and its own graphical symbol, an and symbol with a negation circle after it:
| nand |
Two other very useful functions are nor and xor. The nor gate (short for not or) is a negation of or:
| A | B | A or B | A nor B |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
Its graphical symbol is
| nor |
The last of the named gates that we'll see here is called xor, which stands for exclusive or (as opposed to regular or, which is inclusive). The difference is that where regular or includes the case where both its operands are true, xor does not. An expression A xor B is true when either of its operands are true, but not both:
| A | B | A xor B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Another way to understand xor is to see that it is true if exactly one of the operands is true, and false otherwise. Its graphical symbol is
| xor |
Exercises
- Here is the
diagram for a circuit. Complete the
truth table. The first line has been
done for you as an example.
A B F 0 0 1 0 1 1 0 1 1 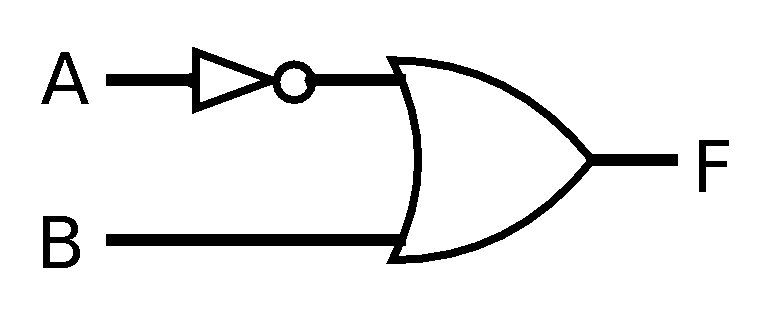
- Here is a
diagram for a circuit. Complete the
truth table. The first line has been
done for you as an example.
A B F 0 0 0 0 1 1 0 1 1 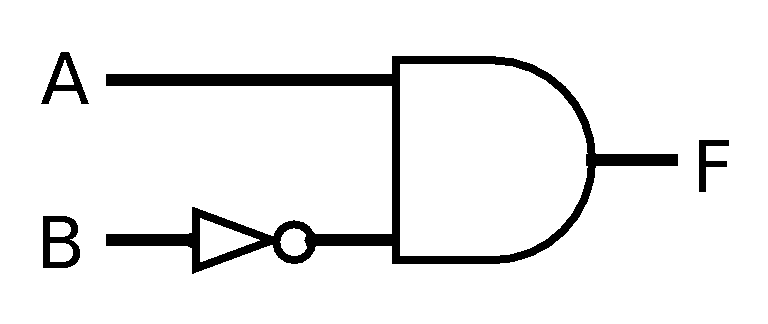
- Here is a
diagram for a circuit. Construct the
truth table.
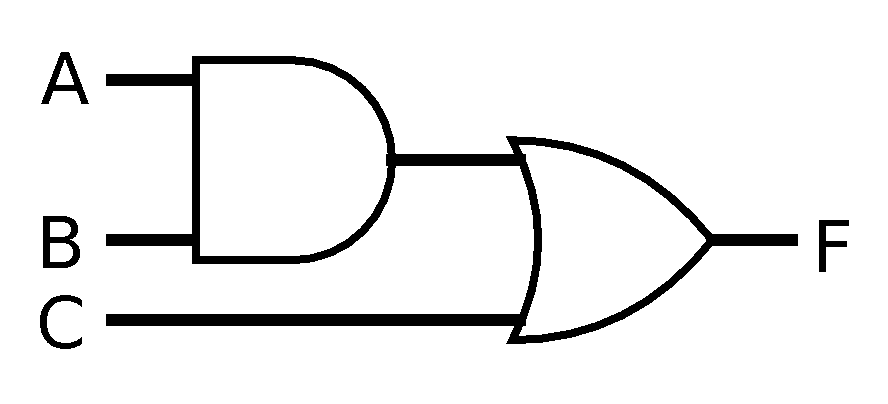
- Here is the
diagram for a circuit. Construct the
truth table.
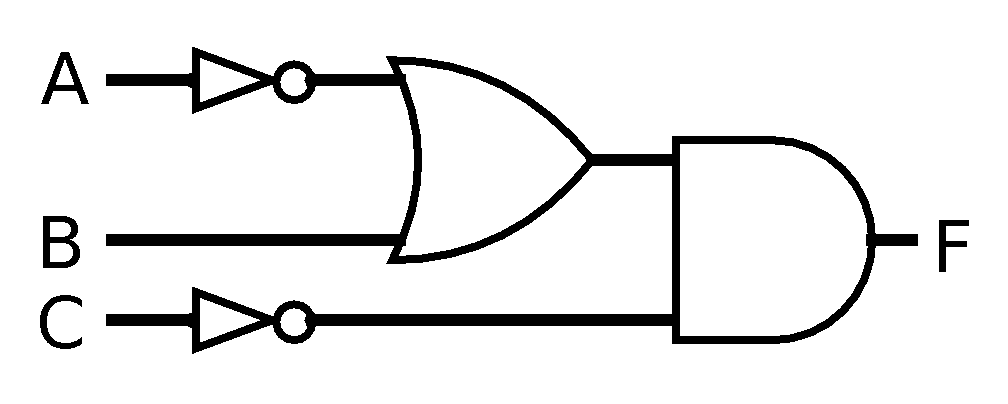
In exercises 5 through 10, write the truth table for the function.
- not (not x)
- not (x or y)
- A and (not B)
- A or (A and B)
- X and (X or Y)
- x and
(x and y)
In exercises 11 through 16, draw a circuit diagram corresponding to the given gate logic expression.
- (A and B) and (not C)
- (A or (not B)) and C
- (A and (not B)) or ((not A) and B)
- (A or (not B)) and (B or (not C))
- (A nand B) or (B nand C)
- (A nor B) and (B xor C)
- Here is the
truth table for a logical function ⇒.
Design a circuit to compute
it using only and,
or,
and not
gates.
A B ⇒ 0 0 1 0 1 1 1 0 0 1 1 1
Credits and licensing
This article is by Robert P. Webber and Don Blaheta, licensed under a Creative Commons BY-SA 3.0 license.
Version 2016-Mar-24 01:00