Building a geodesic torus

small image of torus nets Way back when I was an undergrad, I was a member of the Quincy University math club, and also took a course in polyhedral geometry, both led by Professor Vince Matsko. As a part of one or the other of them, I put together a number of "nets" for assembling card stock paper models of assorted polyhedra and geodesics.

Fast forward to 2005. On a visit to Quincy, Monmouth professor Lyle Welch spotted some of the models we'd put together back then, and as it happened, Vince still had some of the old printouts, which Lyle photocopied and brought back to his students to assemble. On a visit to Monmouth for a math colloquium, Knox professor Andy Leahy spotted my name next to the model (as the "designer"), somewhat to his surprise.

I was pretty surprised too, actually. I hadn't even looked at this stuff in ten years. But I'd kept all my files (through two moves), and sure enough, there was torus.ps, in the "Quincy files" subdirectory of the "Brown files" directory on my current hard drive, still with a last-modified date of Mar 2 1995. Lyle was curious if it could be made to generate geodesic tori of other frequencies.

So I set about re-learning Postscript (it's a programming language, believe it or not, even though it's mostly used as a sort of printer machine code). I had made some efforts at making my original file general, but there were bugs; if you changed some of the parameters, it wouldn't work. A bit of tweaking, and it's all fixed now.

The original torus.ps (for historical reference)
The new torus.ps (6x12)

The "6x12" means that the file will print out six strips, which when cut out, folded, and assembled form one slice making up one twelfth of a torus. To change these numbers, just go in and edit the postscript file with any text editor (vi, TextEdit, Notepad); skip to the bottom and change the numbers under the heading "YOU CAN CHANGE THESE PARAMETERS"---both the number of pieces per slice and the number of slices per torus can be safely increased without changing the page layout (the file will automatically make as many pages as necessary). If you want to decrease either frequency, you may need to tweak the layout so that pieces don't overlap or run off the page; to do that, edit the section "YOU CAN CHANGE THIS IF YOU KNOW WHAT YOU'RE DOING", for which I may at some point post instructions. :)

How it works

A geodesic is the shortest path along a surface between two points; to a first approximation, a "great-circle" path. On a sphere, these geodesics are all pieces of circles that run through the sphere's centre, and in a three-dimensional model you can represent the geodesic with a sector either of that circle or of a corresponding annulus (that is, a ring, although "ring" means something else to algebraicists). The points you connect with the geodesics can be any set of points that all lie on the solid, e.g. icosahedral or something more complicated like a truncated dodecahedron, or something else.

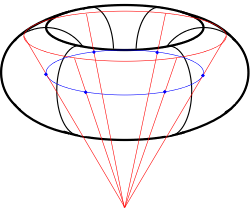torus with conic geodesics So, a torus. A torus is what you get when you take an arbitrary circle and rotate it about an axis that does not intersect it. You can "freeze" the rotation and look at just one of the component circles, and this is one sort of "great circle" path---call it a longitude, because it runs vertically and all such circles are the same size within a given torus. Now restart the rotation, but look at just one point on the rotated circle as it rotates. The circle it traces out is another sort of "great circle"---call it a latitude. As a point of reference, I will also establish the term "circle-of-rotation" to refer to the circle traced out by the centres of all the longitude circles (marked in blue in the diagram to the right).

Calculating the outlines of the ring sectors for the longitude circles is fairly straightforward: they are fragments of a full-circle ring drawn around one point on the circle-of-rotation. If each longitude is to be divided into six parts, each ring sector will be a 60 degree portion of the longitude circle.

The latitude circles are a bit trickier. Two of them---those that lie in the torus plane---are essentially like the longitude rings. But the general case? We want every point on the strip of paper that represents a latitude (red circle in the diagram) to be on a line connecting that latitude with the circle-of-rotation. All such points taken together define a frustum, with the apex of the implied cone lying on the torus' axis of rotation.

Now for a bit of trigonometry. If you look at a cross-section of the torus and cone, as pictured below, you have a diagram that could have come out of basic high-school trig. 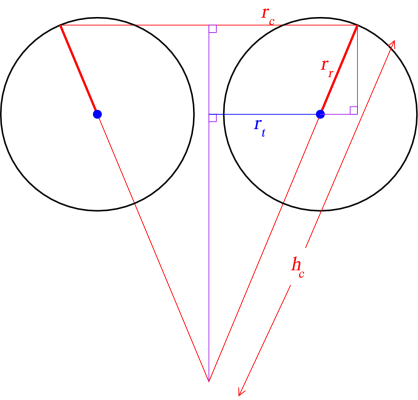unrolled cone As an input to the problem, we'll be given the radius of the circle-of-rotation (r_t) and the radius of the "ring" cross-section of the torus (r_r). When we do the calculations for a given latitude (θ_r), we can compute the radius of the cone as

r_c = r_r cos θ_r + r_t

The hypotenuse of the larger right triangle is the side of the cone (h_c) and can be computed as

h_c = r_t sec θ_r + r_r

unrolled cone Now we need to "unroll" the cone. If we want to make a cone out of a piece of paper, we cut out a sector of a large circle, and bring the straight edges together. The radius of the sectored circle will be h_c, and the entire circumference of the cone's base (c_c) is then just some fraction of the sectored circle's circumference. The sector angle (θ_c) is then calculated using the equation

θ_c / 360° = 2πr_c / 2πh_c

θ_c / 360° = r_c / h_c

The actual angle we need to use will be smaller, since we do not want to generate the entire frustum in one strip; the angle will depend on how many "slices" we wish to make (n_s) into the torus:

θ_s = θ_c / n_t

So at this point, we require five parameters: the radius of the torus; the thickness of the torus (aka the radius of the slice); the width of the strips; the number of slices; and the number of latitudes to take. The default torus.ps has a torus radius of 4 (1 unit is about a half an inch), a slice radius of 2, and a strip width of 1, with 12 slices and 6 latitudes. With those dimensions, we can calculate everything we need to. Each printed strip will have to be a "rectangle" on the torus surface, travelling first along one latitude, then down a longitude, then back along the next latitude, and finally up the original longitude. Though the strip width will be the same for all of these, the radius of the arc will vary, as will the subtended angle. The number of unique strips is dictated by the number of latitudes, as each strip within a slice will be distinct, but each slice is completely identical. Thus, the file need only create the nets for one slice, and it can let a photocopier do the rest of the work.